The desire to optimize performance and guarantee acceptable behaviour in the face of inevitable uncertainty is pervasive throughout control theory. This creates a fundamental challenge since the necessity of stable yet robust control schemes often favors conservative designs, while the desire to optimize performance typically demands the opposite. Two important tools enabling analysis of these issues are input-output and Lyapunov stability theory, but input-output stability theory is particularly amenable when working with nonlinear systems subject to disturbances and noise.
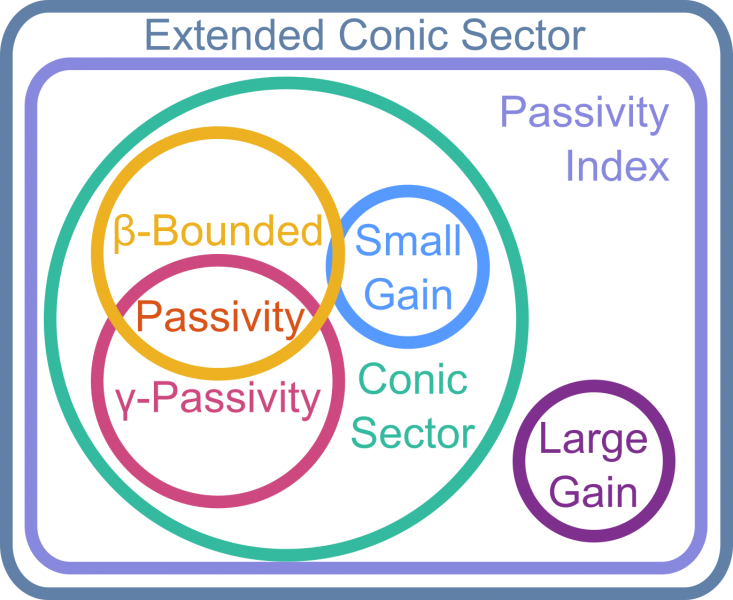
Despite the importance of input-output stability theory to robust and optimal control, its theoretical power has been obscured by an over-reliance on two popular results, the Small Gain and Passivity Theorems. This research focuses on how more general results, such as George Zames' Conic Sector Theorem and notions of dissipativity, can aid in solving the most challenging of modern control problems. The aim is to develop novel controller synthesis and closed-loop stability analysis methods that are readily applicable in practice. Future advances in input-output stability theory are envisioned to exploit numerical error estimates and information about vulnerability to disturbances and uniqueness of responses. The consequences of this research promise to be far-reaching and applications include robotic, delayed, event-triggered, and even open-loop unstable, nonminimum phase systems.