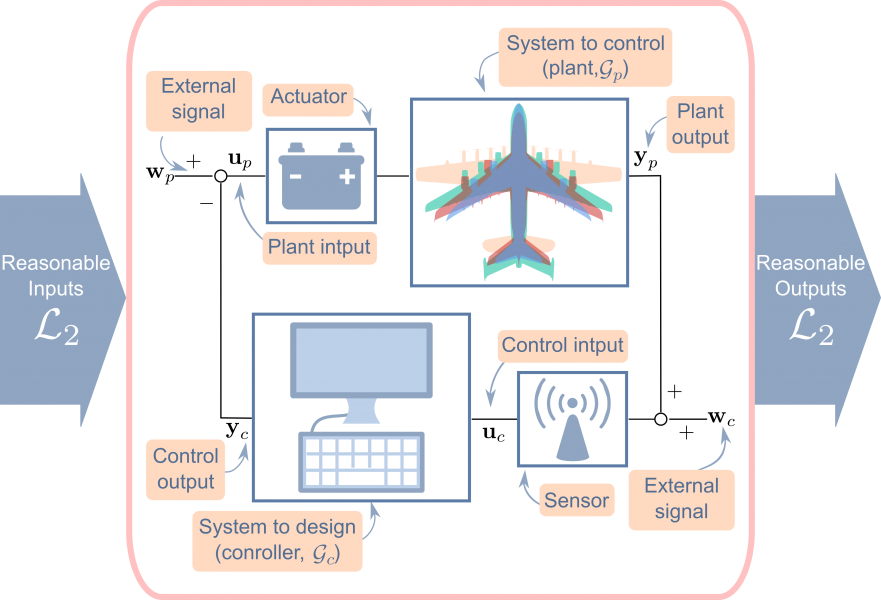
The study of feedback control is arguably the most influential of engineering disciplines. Autonomous driving, spacecraft pointing, indoor temperature and humidity control, and modern cancer radiation therapy all hinge on the ability of a control system to robustly and reliably regulate system behaviour. Despite its diverse areas of application, the desire to optimize performance and guarantee acceptable behavior in the face of inevitable uncertainty is pervasive throughout control theory. This creates a fundamental challenge since the necessity of stable yet robust control schemes often favors conservative designs, while the desire to optimize performance typically demands the opposite. Our research uses the tools of applied mathematics to find the ideal balance between these competing priorities.